KMP字符串匹配算法

第一次接触KMP不是大学学数据结构的时候，而是后来考研接触的，但是当时没弄明白，只会做题（= = 现在工作闲下来, 做leetcode又碰到，不想再糊弄了，得整理下，虽然学完对现在的工作没啥帮助。

简单介绍

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)。

字符串的模式匹配是对字符串的基本操作之一，广泛应用于生物信息学、信息检索、拼写检查、语言翻译、数据压缩、网络入侵检测等领域，如何简化其复杂性一直是算法研究中的经典问题。字符串的模式匹配实质上就是寻找模式串P是否在主串T 中，且其出现的位置。我们对字符串匹配的效率的要求越来越高，应不断地改良模式匹配算法，减少其时间复杂度。

KMP算法是由D.E. Knuth、J.H.Morris和V.R. Pratt提出的，可在一个主文本字符串S内查找一个词W的出现位置。此算法通过运用对这个词在不匹配时本身就包含足够的信息来确定下一个匹配将在哪里开始的发现，从而避免重新检查先前匹配的字符。这个算法是由高德纳和沃恩·普拉特在1974年构思，同年詹姆斯·H·莫里斯也独立地设计出该算法，最终由三人于1977年联合发表。该算法减少了BF算法中i回溯所进行的无谓操作，极大地提高了字符串匹配算法的效率。

来自百度百科

算法描述

在KMP之前是朴素算法：一个主串，一个匹配串，从主串第一位开始比对匹配串，如果没找到就从主串的下一位继续从头开始对比匹配串，没错，如果第一位比对失败那么就从主串后一位继续从匹配串第一位重新开始比对，这就是朴素算法的效率很低的原因。

KMP算法的策略是，找到对比失败时前缀后缀，把前缀推到后缀的位置（指针在变，不在内存中推，为了形象说明😀），减少比对的次数，进而提升效率。为了形象些是前缀后缀的这么说，但具体的实现是在前缀后缀的基础上构建一个next数组来实现位置的跳转。（也就是“推”这一抽象概念）。

那么在说next之前先看一下前缀后缀的效果：

位置	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
haystack	a	b	a	c	a	a	b	a	c	a	b	a	c	a	b	a	a	b	b
needle	a	b	a	c	a	b

现在第6位不匹配，观察needle的前五位，前后都有“a”，这就是最长的前缀了，那么就要把第一位置的“a”推到第五个位置上，如下：

位置	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
haystack	a	b	a	c	a	a	b	a	c	a	b	a	c	a	b	a	a	b	b
needle					a	b	a	c	a	b

来看看这样的一个操作的效果怎么样，我们会发现当前后缀重合后，我们只需要比对重合部分后边的值就可以了，单从这个例子来说，如果用朴素的方法来比对，将需要更多的操作，高下立现。试想，如果给咋们人类两个串，是不是也不会挨个看😅

next数组

上例说了KMP策略的高效之处，那么如何跳转到前后缀的位置就成为这个算法的关键之处。这需要我们在比对前针对needle串（模式串pattern）来构建一个next数组，记录位置信息，也就是当某一个字符与主串不匹配时，我们应该知道j指针要移动到哪？

以下是摘抄参考博客的一部分，我觉的说的比较清楚。

接下来我们自己来发现 j 的移动规律：

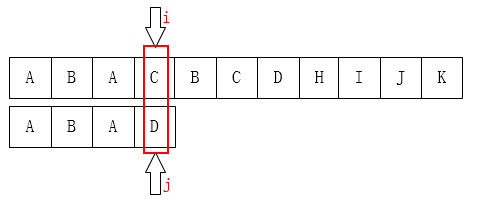
如图：C 和 D不匹配了，我们要把 j 移动到哪？显然是第 1 位。为什么？因为前面有一个 A 相同啊：

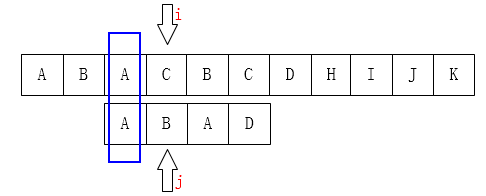
如下图也是一样的情况：

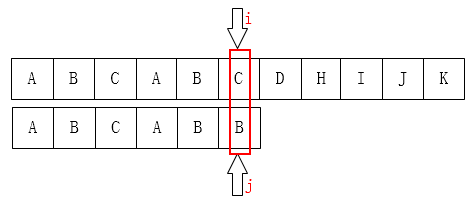
可以把 j 指针移动到第 2 位，因为前面有两个字母是一样的：

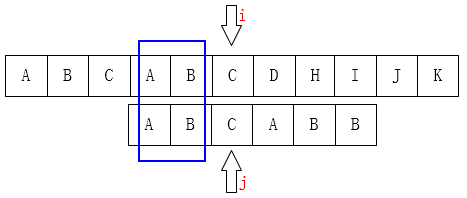
至此我们可以大概看出一点端倪，当匹配失败时，j 要移动的下一个位置 k。存在着这样的性质：最前面的 k 个字符和 j 之前的最后 k 个字符是一样的。

如果用数学公式来表示是这样的:

P[ 0 ~ k-1 ] == P[ j-k ~ j-1] ![KMP5.png](https://i.loli.net/2020/04/16/7bTLykO1Rn9r4wg.png)

下边是next数组的c++代码：

void getnext(string substr, int next[])
{
    int k=-1 , j=0;
    next[0]=-1;  // next 数组第一个位置的数 如果是0的话会无限循环
    while(j<substr.length())
    {
        if(k==-1 || substr[j]==substr[k]) // 为-1的时候j就往后走，k也往后移
        {
            next[++j]=++k;
        }
        else
        {
            k=next[k];
        }
    }
}

尝试过直接生成部分值匹配表，但因为把数组的第一位设为0就一直在死循环。B站上有一个KMP的视频介绍的是部分匹配值表而不是next数组，但我认为差不多，那个视频很好的理解了KMP。不过实现的时候会有死循环的情况。

根据参考资料总结了一个表。

位置	0	1	2	3	4	5	备注
模式串	a	b	a	c	a	b	需要匹配的模式串
部分匹配值	0	0	1	0	1	1	把最后一项删掉前边补上-1，后成了next数组
NEXT数组	-1	0	0	1	0	1	next数组

拓展

Boyer- Moore算法

在用于查找子字符串的算法当中，BM（Boyer-Moore）算法是目前被认为最高效的字符串搜索算法，它由Bob Boyer和J Strother Moore设计于1977年。一般情况下，比KMP算法快3-5倍。该算法常用于文本编辑器中的搜索匹配功能，比如大家所熟知的GNU grep命令使用的就是该算法，这也是GNU grep比BSD grep快的一个重要原因。