神经网络优化（4）正则化

发表于 | 分类于

中国大学mooc课程笔记：《人工智能实践：Tensorflow笔记》曹健 第四讲：神经网络优化 课程地址 课程地址

过拟合

过拟合：神经网络模型在训练数据集上的准确率较高，在新的数据进行预测或分类时准确率较 低，说明模型的泛化能力差。

正则化

正则化：在损失函数中给每个参数 w 加上权重，引入模型复杂度指标，从而抑制模型噪声，减小过拟合。

使用正则化后，损失函数 loss 变为两项之和：

loss = loss(y 与 y_) + REGULARIZER*loss(w)

其中，第一项是预测结果与标准答案之间的差距，如之前讲过的交叉熵、均方误差等；第二项是正则化计算结果。

正则化计算方法：

① L1 正则化： 𝒍𝒐𝒔𝒔𝑳𝟏 = ∑𝒊 𝒘𝒊

用 Tesnsorflow 函数表示:loss(w) = tf.contrib.layers.l1_regularizer(REGULARIZER)(w)

② L2 正则化： 𝒍𝒐𝒔𝒔𝑳𝟐 = ∑𝒊 𝒘𝒊 ²

用 Tesnsorflow 函数表示:loss(w) = tf.contrib.layers.l2_regularizer(REGULARIZER)(w)

用 Tesnsorflow 函数实现正则化：

1
2
tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(regularizer)(w) 
loss = cem + tf.add_n(tf.get_collection('losses'))

cem （交叉熵cd+softmax函数）的计算已在 → 4.1 节中给出

举例：

用 300 个符合正态分布的点 X[x0, x1]作为数据集，根据点 X[x0, x1]计算生成标注 Y_，将数据集标注为红色点和蓝色点。 标注规则为：当 x02 + x12 < 2 时，y_=1，标注为红色；当 x02 + x12 ≥2 时，y_=0，标注为蓝色。 我们分别用无正则化和有正则化两种方法，拟合曲线，把红色点和蓝色点分开。在实际分类时，如果前向传播输出的预测值 y 接近 1 则为红色点概率越大，接近 0 则为蓝色点概率越大，输出的预测值 y 为 0.5 是红蓝点概率分界线。

matplotlib 模块

Python 中的可视化工具模块，实现函数可视化

函数 plt.scatter（）：利用指定颜色实现点(x,y)的可视化

1
2
plt.scatter (x 坐标, y 坐标, c=”颜色”)  
plt.show()

收集规定区域内所有的网格坐标点：

1
2
xx, yy = np.mgrid[起:止:步长, 起:止:步长]  #找到规定区域以步长为分辨率的行列网格坐标点 
grid = np.c_[xx.ravel(), yy.ravel()]  #收集规定区域内所有的网格坐标点 

1
2
3
plt.contour()函数：告知 x、y 坐标和各点高度，用 levels 指定高度的点描上颜色 
plt.contour (x 轴坐标值, y 轴坐标值, 该点的高度, levels=[等高线的高度]) 
plt.show()

例子程序代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
# 0导入模块，生成模拟数据集
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

BARCH_SIZE = 30
seed = 2
# 基于seed产生随机数
rdm = np.random.RandomState(seed)
# 随机数返回300行2列的矩阵，表示300组坐标点（x0，x1）作为输入数据集
X = rdm.randn(300, 2)
# 从X这个300行2列的矩阵中取出一行，判断如果两个坐标的平方和小于2，给Y赋值1，其余复制0 作为输入数据集的标签（正确答案）
Y_ = [int(x0*x0 + x1*x1 < 2) for (x0, x1) in X]

# 遍历Y中的每个元素，1赋值‘red’其余赋值‘blue’，这样可视化显示时人可以直观区分
Y_c = [['red' if y else 'blue'] for y in Y_]
# 对数据集X和标签Y进行shape整理，第一个元素为-1表示，随第二个参数计算得到，第二个元素表示多少列，把X整理为n行2列，
# 把Y整理为n行1列
X = np.vstack(X).reshape(-1, 2)
Y_ = np.vstack(Y_).reshape(-1, 1)
print(X)
print(Y_)
print(Y_c)
# 用plt.scatter画出数据集X各行中第0列元素和第1列元素的点，即各行的（x0，x1），用个行Y_c对应的值表示颜色
plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(Y_c))
plt.show()


# 定义神经网络的输入，参数和输出，定义前向传播过程
def get_weight(shape, regularizer):
    w = tf.Variable(tf.random_normal(shape), dtype=tf.float32)
    tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(regularizer)(w))  # 正则化
    return w


def get_bias(shape):
    b = tf.Variable(tf.constant(0.01, shape=shape))
    return b


x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))

w1 = get_weight([2, 11], 0.01)
b1 = get_bias([11])
y1 = tf.nn.relu(tf.matmul(x, w1) + b1)

w2 = get_weight([11, 1], 0.01)
b2 = get_bias([1])
y = tf.matmul(y1, w2) + b2  # 输出层不过激活函数

# 定义损失函数 正则化是在损失函数中添加权重
loss_mse = tf.reduce_mean(tf.square(y - y_))
loss_total = loss_mse + tf.add_n(tf.get_collection('losses'))

# 定义反向传播方法： 不含正则化
train_step = tf.train.AdamOptimizer(0.0001).minimize(loss_mse)

with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    STEPS = 40000
    for i in range(STEPS):
        start = (i*BARCH_SIZE) % 300
        end = start + BARCH_SIZE
        sess.run(train_step, feed_dict={x:X[start:end], y_:Y_[start:end]})
        if i % 2000 == 0:
            loss_mse_v = sess.run(loss_mse, feed_dict={x:X, y_:Y_})
            print("After %d steps, loss is : %f" % (i, loss_mse_v))
    # xx在-3到3之间以步长为0.01，yy在-3到3之间以步长0.01，生成二维网格坐标点的集合
    xx, yy = np.mgrid[-3:3:.01, -3:3:.01]
    # 将xx， yy拉直，并合并成一个2列的矩阵，得到一个网格坐标点的集合
    grid = np.c_[xx.ravel(), yy.ravel()]
    # 将网格坐标点喂入神经网络，probs为输出
    probs = sess.run(y, feed_dict={x:grid})
    # probs的shape调成xx的样子
    probs = probs.reshape(xx.shape)
    print("w1:\n",sess.run(w1))
    print("b1:\n", sess.run(b1))
    print("w2:\n", sess.run(w2))
    print("b2:\n", sess.run(b2))

plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(Y_c))
plt.contour(xx, yy, probs, levels=[.5])
plt.show()


# 定义反向传播方法：包含正则化
train_step = tf.train.AdamOptimizer(0.0001).minimize(loss_total)

with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    STEPS = 40000
    for i in range(STEPS):
        start = (i * BARCH_SIZE) % 300
        end = start + BARCH_SIZE
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y_[start:end]})
        if i % 2000 == 0:
            loss_v = sess.run(loss_total, feed_dict={x: X, y_: Y_})
            print("After %d steps, loss is : %f" % (i, loss_v))

    # xx在-3到3之间以步长为0.01，yy在-3到3之间以步长0.01，生成二维网格坐标点的集合
    xx, yy = np.mgrid[-3:3:.01, -3:3:.01]
    # 将xx， yy拉直，并合并成一个2列的矩阵，得到一个网格坐标点的集合
    grid = np.c_[xx.ravel(), yy.ravel()]
    # 将网格坐标点喂入神经网络，probs为输出
    probs = sess.run(y, feed_dict={x: grid})
    # probs的shape调成xx的样子
    probs = probs.reshape(xx.shape)
    print("w1:\n", sess.run(w1))
    print("b1:\n", sess.run(b1))
    print("w2:\n", sess.run(w2))
    print("b2:\n", sess.run(b2))

plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(Y_c))
plt.contour(xx, yy, probs, levels=[.5])
plt.show()

两次运行结果：

RUN_first：

不使用正则化：

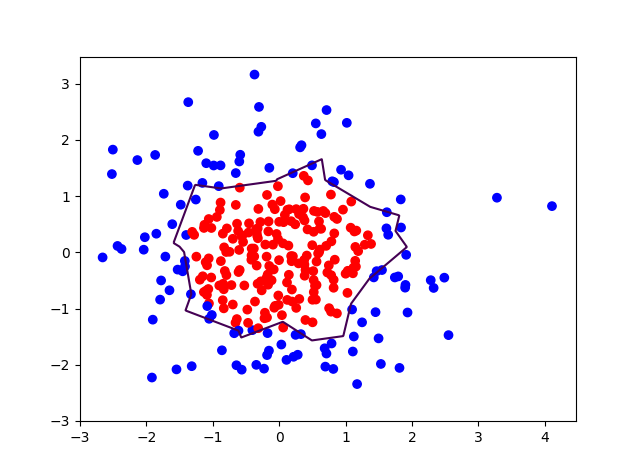
Figure_1.png

使用正则化：

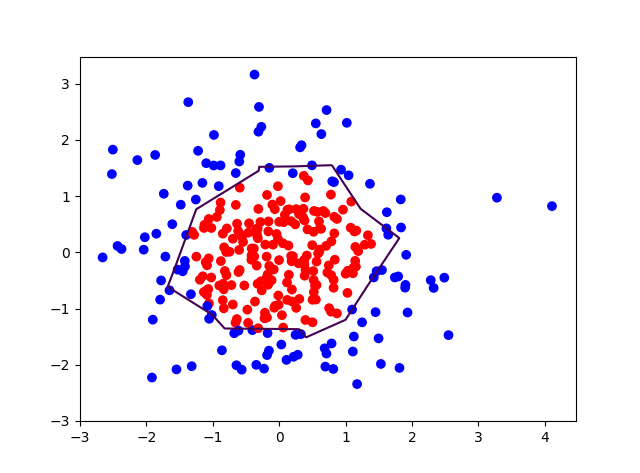
Figure_1-1.png

RUN_second：

不使用正则化：

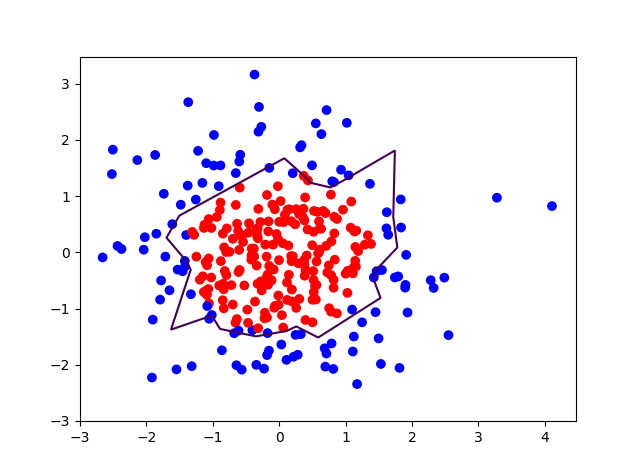
Figure_2.png

使用正则化：

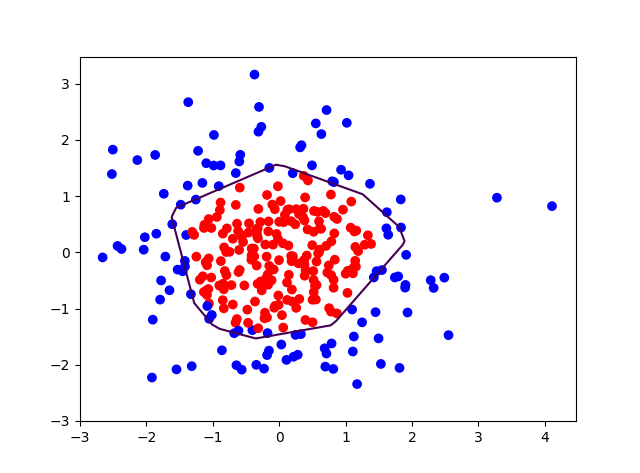
Figure_2-2.png

对比无正则化与有正则化模型的训练结果，可看出有正则化模型的拟合曲线平滑，模型具有更好的泛化能力。第二次的运行对比比较明显，不适用正则化的曲线会有“突刺”，而使用正则化则比较平滑。

总结

在运行代码的时候出现没有系统报错，但是运行的时间比较久超过了10分钟，开始想可能是参数错误，但是看到那些输出的消息不是对应的print函数中的内容，思索无果，于是重新对比代码，发现原来是缩进错误，在代码的70~81和103~114行多缩进了两位，导致代码段被for函数囊括，输出了很多无意义的内容。修改缩进后，程序正常运行，可见python的缩进特征带写代码的时候要特别注意一下。

整体来说对正则化的了解还停留在“在损失函数中添加权重”的水平下，仍需多理解。我觉得这mooc这个课程对知识原理得讲解还是不太够，我得基础也不太好，所以买了一本书《Python强化学习实战：应用OpenAI Gym和TensorFlow精通强化学习和深度强化学习》机械工业出版社出版，后续会在更新读书笔记。

在者关于学习环境，在宿舍有电给电脑充电，实际也可以学习，可是思想容易涣散，自己不够专注。这时，只要有点像跑题，就收拾一下去图书馆吧，真心可以专注一些小目标的实现。比方说写一篇博客，整理下内容，读一篇文章，听一段课…这些小内容在图书馆执行得效率特别高，用时也短，所以电脑的电量也够。如果不够得话，这样也有一个具体得任务可以到宿舍在办，有这个小任务约束住自己得思想，在宿舍也就更能控制自己了。