Tensorflow框架(3)反向传播

发表于 | 分类于

中国大学mooc课程笔记：《人工智能实践：Tensorflow笔记》曹健 第三讲：Tensorflow框架 课程地址

基于Tensorflow的NN： 用张量表示数据,用计算图搭建神经网络，用会话执行计算图，优化线上的权重（参数），得到模型。

反向传播

反向传播：训练模型参数，在所有参数上用梯度下降，使 NN 模型在训练数据 上的损失函数最小。

损失函数（loss）：计算得到的预测值 y 与已知答案 y_的差距。损失函数的计算有很多方法，均方误差 MSE 是比较常用的方法之一。

prt5.png

用 tensorflow 函数表示为：

1
loss_mse = tf.reduce_mean(tf.square(y_ - y))

反向传播训练方法：以减小 loss 值为优化目标，有梯度下降、momentum 优化 器、adam 优化器等优化方法。

这三种优化方法用 tensorflow 的函数可以表示为：

1
2
3
train_step=tf.train.GradientDescentOptimizer(learning_rate).minimize(loss) 
train_step=tf.train.MomentumOptimizer(learning_rate, momentum).minimize(loss) 
train_step=tf.train.AdamOptimizer(learning_rate).minimize(loss)

三种优化方法区别如下：

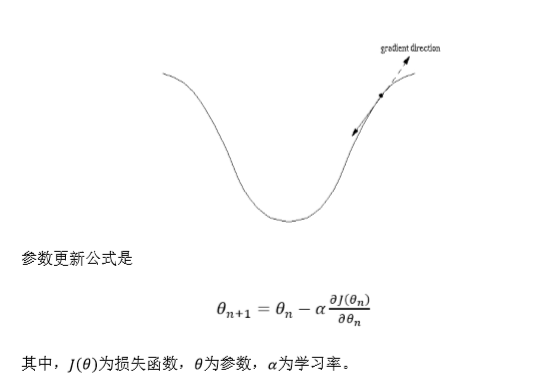
  1. tf.train.GradientDescentOptimizer()使用随机梯度下降算法，使参数沿着 梯度的反方向，即总损失减小的方向移动，实现更新参数。

prt6.png

2. tf.train.MomentumOptimizer()在更新参数时，利用了超参数，参数更新公式 是

prt7.png

3. tf.train.AdamOptimizer()是利用自适应学习率的优化算法，Adam 算法和随 机梯度下降算法不同。随机梯度下降算法保持单一的学习率更新所有的参数，学 习率在训练过程中并不会改变。而 Adam 算法通过计算梯度的一阶矩估计和二 阶矩估计而为不同的参数设计独立的自适应性学习率。

学习率：决定每次参数更新的幅度。

优化器中都需要一个叫做学习率的参数，使用时，如果学习率选择过大会出现震 荡不收敛的情况，如果学习率选择过小，会出现收敛速度慢的情况。我们可以选 个比较小的值填入，比如 0.01、0.001。

搭建神经网络的八股

prt8.png

举例

随机产生 32 组生产出的零件的体积和重量，训练 3000 轮，每 500 轮输出一次损 失函数。下面我们通过源代码进一步理解神经网络的实现过程： 0.导入模块，生成模拟数据集；

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# 0导入模块，生成模拟数据集。
import tensorflow as tf
import numpy as np
BATCH_SIZE = 8
seed = 23455

# 基于seed产生随机数
rng = np.random.RandomState(seed)
# 随机数返回32行2列的矩阵 表示32组 体积和重量 作为输入数据集
X = rng.rand(32, 2)
# 从X这个32行2列的矩阵中 取出一行 判断如果和小于1 给y赋值1 如果和不小于1 赋值为0
# 作为输入数据集的标签（正确答案）
Y = [[int(x0 + x1 < 1)] for (x0, x1) in X]
print("X:\n", X)
print("Y:\n", Y)

# 1定义神经网络的输入，参数和输出，定义前向传播过程。
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))

w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))

a = tf.matmul(x, w1)
y = tf.matmul(a, w2)

# 2定义损失函数及反向传播方法
loss = tf.reduce_mean(tf.square(y - y_))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)
# train_step = tf.train.MomentumOptimizer(0.001, 0.9).minimize(loss)
# train_step = tf.train.AdadeltaOptimizer(0.001).minimize(loss)

# 3生成对话，训练STEP轮
with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    # 输出目前未经训练的参数取值。
    print("w1:\n", sess.run(w1))
    print("w2:\n", sess.run(w2))
    print("\n")

    # 训练模型
    STEPS = 3000
    for i in range(STEPS):
        start = (i*BATCH_SIZE) % 32
        end = start + BATCH_SIZE
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
        if i % 500 == 0:
            total_loss = sess.run(loss, feed_dict={x: X, y_: Y})
            print("After %d training step(s), loss on all data is %g" % (i, total_loss))

    # 输出训练后的参数取值
    print("\n")
    print("w1:\n", sess.run(w1))
    print("w2:\n", sess.run(w2))

GradientDescentOptimizer:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
After 0 training step(s), loss on all data is 5.13118
After 500 training step(s), loss on all data is 0.429111
After 1000 training step(s), loss on all data is 0.409789
After 1500 training step(s), loss on all data is 0.399923
After 2000 training step(s), loss on all data is 0.394146
After 2500 training step(s), loss on all data is 0.390597


w1:
 [[-0.70006633  0.9136318   0.08953571]
 [-2.3402493  -0.14641267  0.58823055]]
w2:
 [[-0.06024267]
 [ 0.91956186]
 [-0.0682071 ]]

MomentumOptimizer：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
After 0 training step(s), loss on all data is 5.13118
After 500 training step(s), loss on all data is 0.384391
After 1000 training step(s), loss on all data is 0.383592
After 1500 training step(s), loss on all data is 0.383562
After 2000 training step(s), loss on all data is 0.383561
After 2500 training step(s), loss on all data is 0.383561


w1:
 [[-0.61332554  0.8312484   0.07565959]
 [-2.25777149 -0.14481366  0.56783187]]
w2:
 [[-0.10432342]
 [ 0.77349013]
 [-0.04419039]]

AdadeltaOptimizer:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
After 0 training step(s), loss on all data is 5.23347
After 500 training step(s), loss on all data is 5.22724
After 1000 training step(s), loss on all data is 5.21959
After 1500 training step(s), loss on all data is 5.21088
After 2000 training step(s), loss on all data is 5.20146
After 2500 training step(s), loss on all data is 5.19155


w1:
 [[-0.80936033  1.48264468  0.06338602]
 [-2.44044113  0.09701534  0.58901256]]
w2:
 [[-0.80885708]
 [ 1.48254037]
 [ 0.06299981]]

不同反向传播方法对loss的收敛影响很大，第三个方法与前两个差的很多，也许是当前问题不适合用那种解法。要具体问题具体具体分析。通过这节课，使用tensorflow的基本语法和算法结构都有了些了解，感觉像是在向一种神秘的宝藏慢慢探索，一点一点解密似的。另外，jekyll writer的使用慢慢熟悉了,但markdown的语法还只是掌握了一小部分，慢慢来呗。在最后作个对联：

上联：阳春白雪刮大风
下联：冷冷冷冷冷冷冷
横批：多喝热水